杠杆平衡条件应用

杠杆原理深度解析

一、杠杆的基本概念

杠杆是一种简单机械，由一个支点、一个动力臂和一个阻力臂组成。通过改变动力臂和阻力臂的长度比例，可以实现力的放大或减小。

二、杠杆的平衡条件

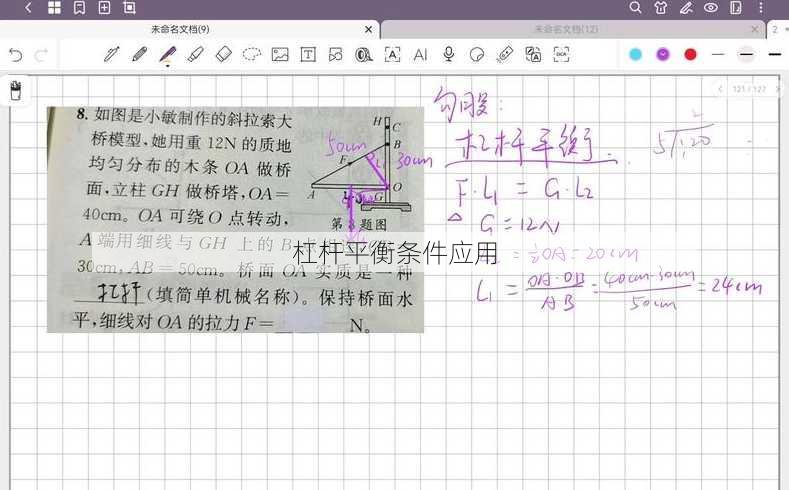
杠杆的平衡条件可以用以下公式表示：

[ F1 times L1 F2 times L2 ]

其中，( F1 ) 和 ( F2 ) 分别是动力和阻力，( L1 ) 和 ( L2 ) 分别是动力臂和阻力臂的长度。

三、杠杆的分类

1. 第一类杠杆：动力作用在支点和阻力之间，如撬棍。

2. 第二类杠杆：阻力作用在支点和动力之间，如剪刀。

   

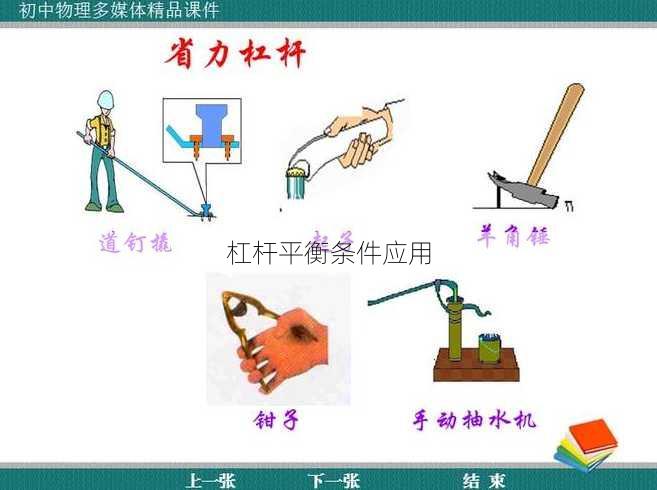
3. 第三类杠杆：动力和阻力都作用在支点的同一侧，如鱼竿。

四、杠杆的应用实例

1. 撬棍：通过增加动力臂的长度，可以减小所需的动力，使得举起重物变得容易。

2. 剪刀：通过设计剪刀的杠杆比，使得剪切纸张等物体更加省力。

3. 鱼竿：鱼竿的杠杆比设计使得钓鱼时可以施加较小的力，却可以捕捞到较大的鱼。

五、杠杆问题解答

1. 问题：一根杠杆的支点位于中间，动力臂长度为10cm，阻力臂长度为5cm。若动力为10N，求阻力的大小。

回答：根据杠杆的平衡条件，( F1 times L1 F2 times L2 )，代入数值得到 ( 10N times 10cm F2 times 5cm )，解得 ( F2 20N )。

2. 问题：一把剪刀的动力臂长度为20cm，阻力臂长度为10cm。若阻力为5N，求所需动力的大小。

回答：同样根据杠杆的平衡条件，代入数值得到 ( F1 times 20cm 5N times 10cm )，解得 ( F1 2.5N )。

3. 问题：一个撬棍的动力臂长度为30cm，阻力臂长度为15cm。若动力为15N，求撬棍能撬起的最大重物的重量。

回答：根据杠杆的平衡条件，代入数值得到 ( 15N times 30cm F2 times 15cm )，解得 ( F2 30N )。撬棍能撬起的最大重物的重量为30N。

4. 问题：一个鱼竿的动力臂长度为100cm，阻力臂长度为20cm。若阻力为2N，求钓鱼时所需的动力大小。

回答：根据杠杆的平衡条件，代入数值得到 ( F1 times 100cm 2N times 20cm )，解得 ( F1 0.4N )。钓鱼时所需的动力大小为0.4N。

5. 问题：一个学生的书包挂在课桌的挂钩上，书包的重力为20N，挂钩到书包的距离为30cm。若学生用50cm长的绳子拉书包，求绳子所需的拉力大小。

回答：这是一个复合杠杆问题。首先计算书包的重力作用点距离支点的距离，即 ( 30cm + 50cm 80cm )。然后根据杠杆的平衡条件，代入数值得到 ( F1 times 50cm 20N times 80cm )，解得 ( F1 40N )。绳子所需的拉力大小为40N。